

Thus, there is a reasonable chance that the intercept is actually zero, because the estimated range spans zero. The probability that the true value of the intercept is in the range 1.5 - 2.0 to 1.5 + 2.0 is approximately 67%. What can you deduce about the value of the intercept? The values Excel produces are m = 10.2 and c = 1.5 with standard errors σ m = 3.0 σ c = 2.0. You have performed a least squares regression using Excel and estimated the slope and intercept of the relationship y = mx + c. In other words, the probability that the true value of m falls within the range m - σ m to m + σ m is approximately 67%. The errors in m and c are usually given in the form of standard errors, i.e. These uncertainties are essential information that allows the user to determine how well the straight line fit really represents the relationship between X and Y given that you only sampled a small part of the population. In addition, the least squares method allows one to estimate the uncertainties in the derived values of m and c, together with the correlation coefficient r (-1 < r < 1) that describes the degree of correlation between X and Y.
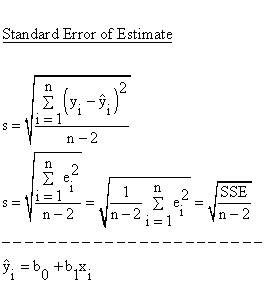
Analytical software packages will output these values (often termed the slope and the intercept). The result is that expressions are found for the values of m and c that minimizes SD. For linear least squares regression, the idea is to find the line y = mx + c that minimizes the mean squared difference between the line and the data points (circles). See Chapter 15 of Numerical Recipes by Press et al., Cambridge University Press, 1992 for full details.įigure 1: Illustration of linear regression. This is achieved by calculating the partial derivatives of SD with respect to m and c and finding the pair such that SD is at a minimum. Taking all the data points, we seek values of m and c that minimize the squared difference SD. Thus, y(x i) - y i is the difference between the line and data point i (see Fig. The straight line relating X and Y is y = mx + c, where m and c are the gradient and constant values (to be determined) defining the straight line. Let, i = 1,2,3,…., N be the N pairs of data values of the variables X and Y. The usual approach is to use the least-squares method, which minimizes the squared difference between the actual data points and a straight line. Excel, Matlab, IDL) have tools to compute linear regression. However, if a reasonable degree of correlation exists between X and Y then linear regression may be a useful means to describe the relationship between the two variables.
If variables X and Y are uncorrelated, it is pointless embarking upon linear regression. Linear regression is a method for determining the best linear relationship between two variables X and Y.
Class Homepage | Labs | Resources | Homework


 0 kommentar(er)
0 kommentar(er)
